Principle Component Analysis
Principal component analysis (PCA) is a model-free method as an important part of unsupervised learning. Because PCA is model-free, it does not rely on any factors such as value, momentum to decompose a portfolio returns. We can use PCA to deduce the structure of portfolio returns to construct market-neutral portfolios; to detect systematic risk; to enable risk management and strategy backtesting.
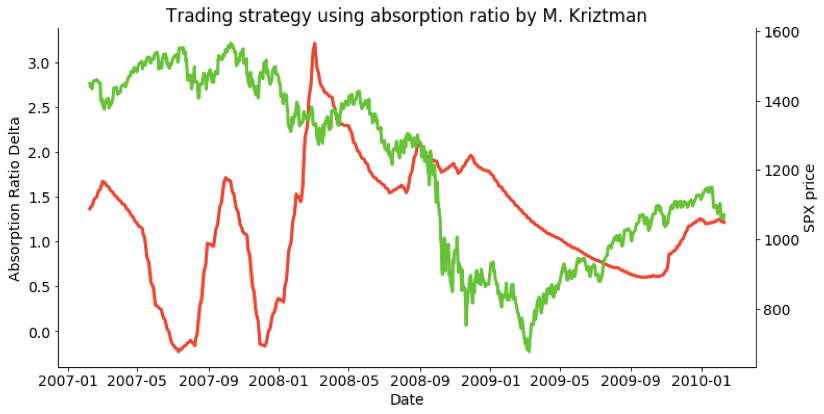
PCA is a statistical procedure using orthogonal transformation in order to convert a set of stock returns (a portfolio) into a set of vectors (portfolios) that are linearly uncorrelated and they are called principal components (PCs).
The first PC has the largest possible variance and mimics the return of the original portfolio. Each succeeding component has the highest variance possible and it is uncorrelated with (or orthogonal to) the preceding components.
Since the second PC is uncorrelated to the first component, we can use it to construct market-neutral portfolio.
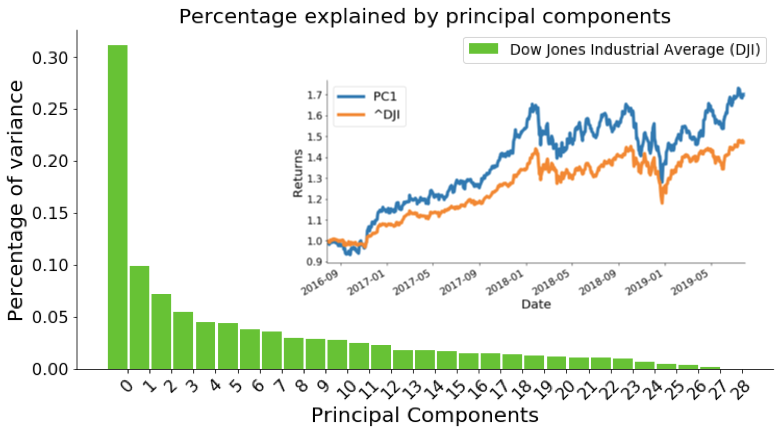
We can use TensorFlow or Keras to perform t-distributed stochastic neighbor embedding (t-SNE) analysis in order to provide a better visualization than PCA.
PCA and neural encoder technique enable us to generate various trading strategies. Neural encoder has layers of artificial neurons or perceptrons and the last layer provides a low-dimensional representation of data.
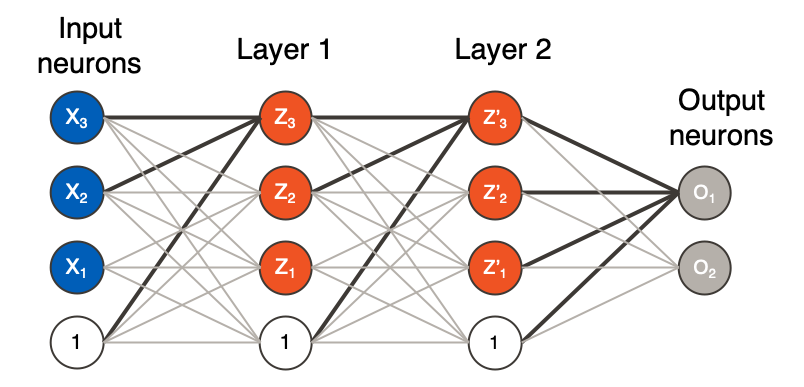
As an example, Mark Kritzman in Principal Components as a measure of systematic risk uses absorption ratio (AR) to define the fraction of the total variance of a stock portfolio that is absorbed by a fixed number of eigenvectors. When the ratio is high, the market is tight and vulnerable to negative shocks; When the ratio is low, the market is less vulnerable to negative shocks. We can use PCA and neural encoder technique through TesnsorFlow to generate absorption ratio, define trading strategies and then backtesting these strategies.